So, we’ve been playing rimworld a lot recently. One of the mods we use is called Rim Factory, which is quite nice overall for building automated bases(yes this breaks the game’s economy, what of it?). One of the mechanics it adds is a buildable object called a sprinkler, which, instead of watering your plants(this isn’t necessary in vanilla rimworld), it causes planets within a certain radius(the second tier is within twelve tiles), to grow by two hours. This is, completely unbalanced and, when you get down to it, just another item in the pursuit of excess, but that’s how we like to play the game.
Anyway, we were wondering about figuring out an optimal pattern for the usage, and since the more rigorous tools we have to measure such things are largely forgotten, we built a little simulation script in python to try and get a feel for various optimization strategies, and the most fun part, of course, is how we went about building this kind of tool.
This tool is remarkably sketchy, it does not attempt to be rigorous, or even follow the watering pattern other than cycling through all of the tiles in range.
Since we’ve been building stuff with python lately, this is in python, which, as always, never ceases to amaze how easy the ecosystem makes it to do this kind of task.
Anyway, to get an idea of where this is going, let’s start with the import block at the top:
from typing import * import numpy as np import itertools import functools import math import statistics import matplotlib import matplotlib.pyplot as plt import random from enum import IntEnum, auto
The building blocks
The core of the script is the iterators that provide the information about where the focus is, and since this is a script without much intention of going particularly far, we can use globals and constants, so let’s start with those!
# The size of the map being kept track of. # # In this case, this means that the map consists of the area from (-24,-24) to (24,24) MAP_SIZE = 24 # The radius of a sprinkler mkii is 12 blocks RADIUS = 12
Iterators
The heart and soul of this program is in its iterators, so let’s start by defining one that will make the rest of our work easier.
def cartesian(start: int, end: int) -> Iterator[Tuple[int,int]]:
"""
Turn a single range iterator as in range(start,end) into a cartesian product
"""
return itertools.product(range(start,end),repeat=2)
That’ll be useful for iterating over the map. The next are a bit less sensible, but, they work, and this isn’t meant to be perfect.
def map_tiles():
r = RADIUS+1
z = itertools.product(range(-MAP_SIZE,MAP_SIZE), repeat=2)
z = list(z)
random.shuffle(z)
for x in z:
yield x
def sprinkler(position:Tuple[int,int]) -> Iterator[Tuple[int,int]]:
for i, j in cartesian(0, RADIUS+1):
if i==0 and j == 0:
continue
s = i**2+j**2
if math.sqrt(s) <= RADIUS:
yield (i+position[0], j+position[1])
yield (position[0]+i,position[1]-j)
yield (position[0]-i,j+position[1])
yield (position[0]-i,position[1]-j)
Fitness
Next comes the fitness function, which, to start off with, will just be a simple mean of how many times each tile has been hit by a sprinkler.
def evaluate_fitness(field: Dict[Tuple[int,int], int]) -> float:
return sum(field.values()) / (2*MAP_SIZE)**2
Each round in the simulation consists of iterating across a given number of sprinklers n times, and is called for each candidate to figure out the best one.
Putting that together
def simulate(positions: Iterable[Tuple[int,int]], rounds: int)\
-> Dict[Tuple[int,int],int]:
field = {(x,y):0 for x,y in cartesian(-MAP_SIZE, MAP_SIZE)
if (x,y) not in positions}
for i in positions:
if i in field:
del field[i]
sprinklers = list(map(lambda x: itertools.cycle(sprinkler(x)), positions))
for _ in range(rounds):
for s in sprinklers:
pos = next(s)
if pos in field:
field[pos] += 1
return field
So now that we can evaluate each choice we might make, we have to make it possible to put these together for any number of sprinklers, so we write another function called evaluate_alternatives. Here we decided to limit the breadth of each search step to a given number, here it’s called to_try.
def evaluate_alternatives(positions: Iterable[Tuple[int,int]],
to_try: int,
rounds: int) -> List[Tuple[int,int]]:
# Eliminate already extant positions
options = set(map_tiles()) - set(positions)
options = list(options)
random.shuffle(options)
to_try = min(to_try, len(options)-1)
options = options[0:to_try]
best_fitness = -2**48
best_found = None
for i in options:
f = simulate(positions + [i], rounds)
fitness = evaluate_fitness(f)
if fitness > best_fitness:
best_found = i
best_fitness = fitness
print(f"best fitness found this round {best_fitness}")
return positions + [best_found]
Next we put together the final pieces in a function we called optimize.
def optimize(n: int, candidates:int, rounds: int):
positions = []
while len(positions) < n:
positions = evaluate_alternatives(positions, candidates, rounds)
fields = simulate(positions, rounds)
heatmap = np.array([[(fields[x,y] if (x,y) in fields else -5)
for x in range(-MAP_SIZE, MAP_SIZE)]
for y in range(-MAP_SIZE,MAP_SIZE)])
fig, ax = plt.subplots()
im = ax.imshow(heatmap)
# You can uncomment these if you want to have a label on each cell in the heatmap,
# for 48x48, it is rather overwhelming
## for (x,y), v in fields.items():
## ax.text(x+MAP_SIZE,y+MAP_SIZE, math.floor(fields[x,y]), ha='center', va='center', color='w')
fig.tight_layout()
plt.show()
and to top it off, we invoke it at the end of the file:
optimize(10, 80, 1500)
The output should then look something like this
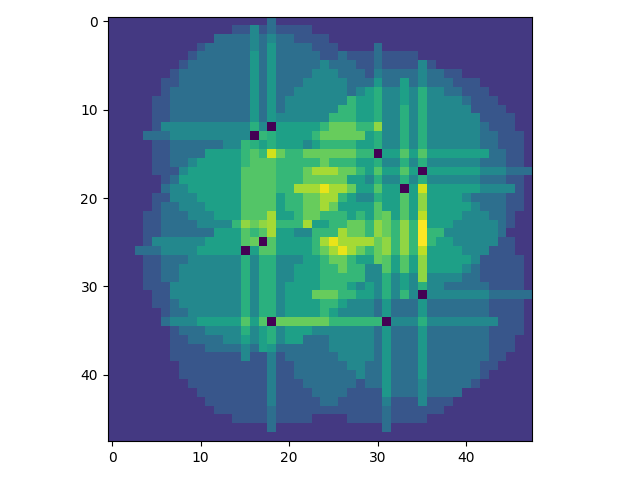
Okay, that’s fine, but it’s not necessarily what you might want from such a tool. What if you’d rather have as much coverage as possible with a given number of sprinklers?
Well, we can do that.
Alternative fitness metrics
Okay, so what we need to optimize for to get the best coverage possible is to simply count the fields which are touched. In all likelihood, we might end up wanting further metrics to measure by, so we might as well make it a bit… well… Configurable, if you’re going to use a charitable term. So let’s introduce an Enum right before the fitness function.
class FitnessMetric(IntEnum):
MEAN = auto()
COVERAGE = auto()
fitness_metric = FitnessMetric.COVERAGE
Then we need to modify the evaluate_fitness function.
def evaluate_fitness(field: Dict[Tuple[int,int],int]) -> float:
if fitness_metric == FitnessMetric.COVERAGE:
r = len(list(filter(lambda x:x>0, field.values())))
elif fitness_metric == FitnessMetric.MEAN:
r = sum(field.values())/(2*MAP_SIZE)**2
return r
Let’s run the script again and see what falls out.
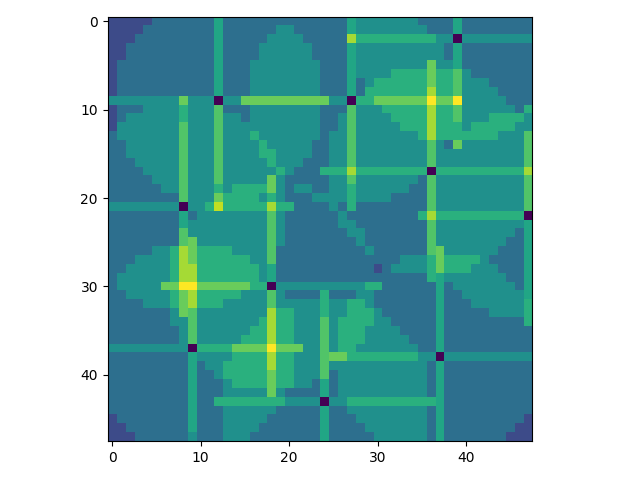
That certainly seems to have the right effect. The majority of the map is covered by the sprinklers.
Complications
So, if you’re familiar with this mod, you might realize there are some things this isn’t even trying to account for, namely any infrastructure. Well, that should be easy to add. 🤞
Let’s add a set of positions that we don’t want filled. For now, let’s leave it to the center(we’re assuming that maybe you have a harvester station set up there), so let’s add another constant in front of evaluate_alternatives (yeah, this is getting pretty messy).
excluded_positions = frozenset([(0,0)])
Then we just have to modify evaluate_alternatives to avoid these positions.
def evaluate_alternatives(positions: Iterable[Tuple[int,int]],
to_try: int,
rounds: int) -> List[Tuple[int,int]]:
# Eliminate already extant positions
options = set(map_tiles()) - set(positions) - excluded_positions
# --- SNIP ---
heatmap = np.array([[(fields[x,y] if (x,y) in fields and (x,y) not in excluded_positions else -5)
for x in range(-MAP_SIZE, MAP_SIZE)]
for y in range(-MAP_SIZE,MAP_SIZE)])
# --- SNIP ---
Alright, what does that make it do?
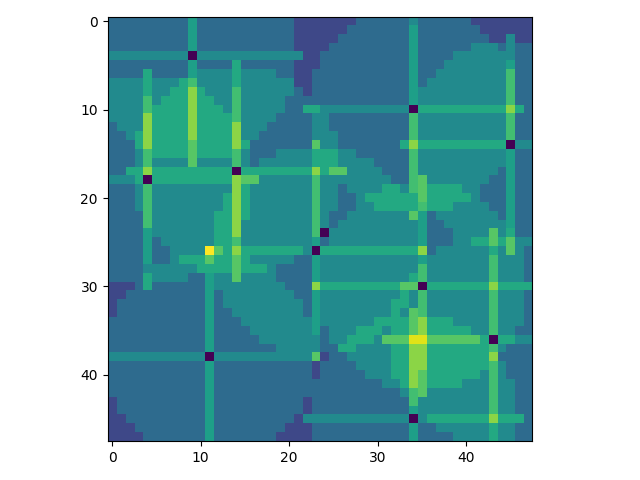
Alright, that’s a further improvement, we suppose, if nothing else it permits more flexibility in terms of describing a given scenario you want to optimize for.
Okay, so let’s say that you have a specific area that you want to optimize coverage for. How would we go about adding that?
Well, at this point it’s pretty clear that all this nonsense with enums is going to be an increasingly weak abstraction for dealing with additional fitness functions, but let’s keep it for now, if only because we’re not sure how we want to go about fixing this ugly feeling design as of writing this very paragraph.
Okay, so let’s assume that you want to optimize for an automatic harvester with an area between (-5,-5) and (5,5).
special_region = set(cartesian(-5,5))
And we can alter evaluate_fitness to this:
def evaluate_fitness(field: Dict[Tuple[int,int], int]) -> float:
r=0
if fitness_metric == Fitness.MEAN:
r = sum(field.values())/(MAP_SIZE*2)**2
elif fitness_metric == Fitness.COVERAGE:
r = len(list(filter(lambda x:x>0, field.values())))
elif fitness_metric == Fitness.SPECIAL_REGION:
r = sum(map(lambda x:x[1], filter(lambda x: x[0] in special_region,field.items())))
return r
We end up with output like this:
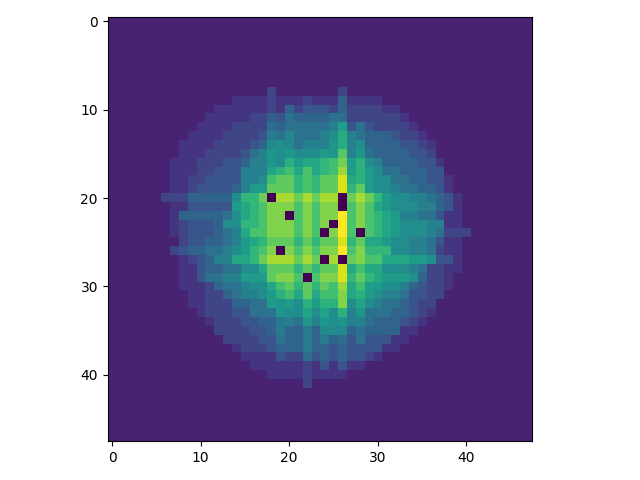
You might not like this output because, among other things, it doesn’t penalize the sprinklers for showing up inside of our growing zone. So, we need to add another line to our much suffering evaluate_fitness function.
def evaluate_fitness(field: Dict[Tuple[int,int], int]) -> float:
r=0
if fitness_metric == Fitness.MEAN:
r = sum(field.values())/(MAP_SIZE*2)**2
elif fitness_metric == Fitness.COVERAGE:
r = len(list(filter(lambda x:x>0, field.values())))
elif fitness_metric == Fitness.SPECIAL_REGION:
r = sum(map(lambda x:x[1], filter(lambda x: x[0] in special_region,field.items())))
r /= max(1, len([(x,y) for x,y in special_region
if (x,y) not in field.keys()
if (x,y) not in excluded_positions]))
return r
And this helps a bit: Let’s label a similar run to see if it has excluded the region altogether, if a square ends up labelled ‘Se’ it indicates that it’s a sprinkler in an excluded area.
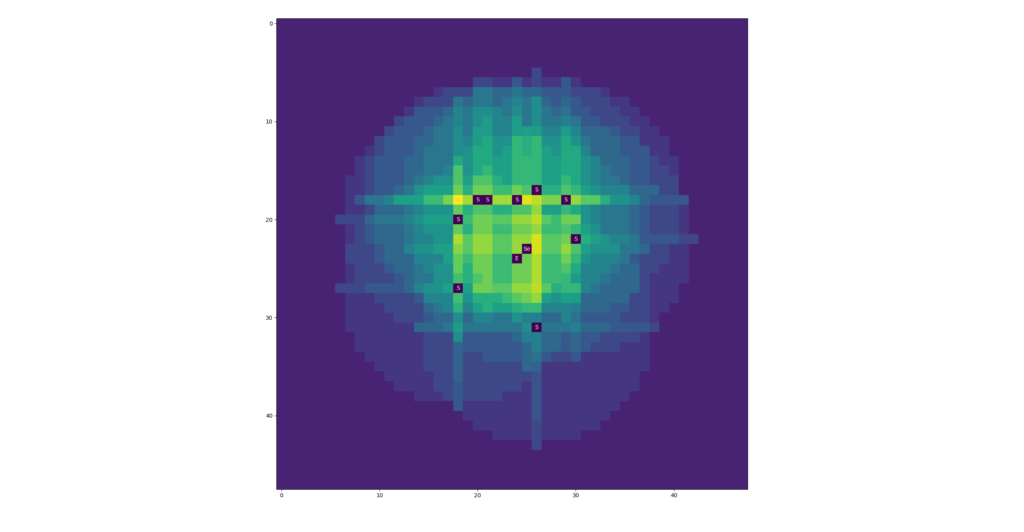
Well, damn. Our code has a mistake in it that permitted the single offending sprinkler. We can fix this by changing the function, to this:
def evaluate_fitness(field: Dict[Tuple[int,int], int]) -> float:
r=0
if fitness_metric == Fitness.MEAN:
r = sum(field.values())/(MAP_SIZE*2)**2
elif fitness_metric == Fitness.COVERAGE:
r = len(list(filter(lambda x:x>0, field.values())))
elif fitness_metric == Fitness.SPECIAL_REGION:
r = sum(map(lambda x:x[1], filter(lambda x: x[0] in special_region,field.items())))
penalty_squares = len([(x,y) for x,y in special_region
if (x,y) not in field.keys()
if (x,y) not in excluded_positions])
r/= penalty_squares+1
return r
Alright, and this fixes that issue(and with another fix applied it labels the spots with sprinklers correctly as ‘S’).
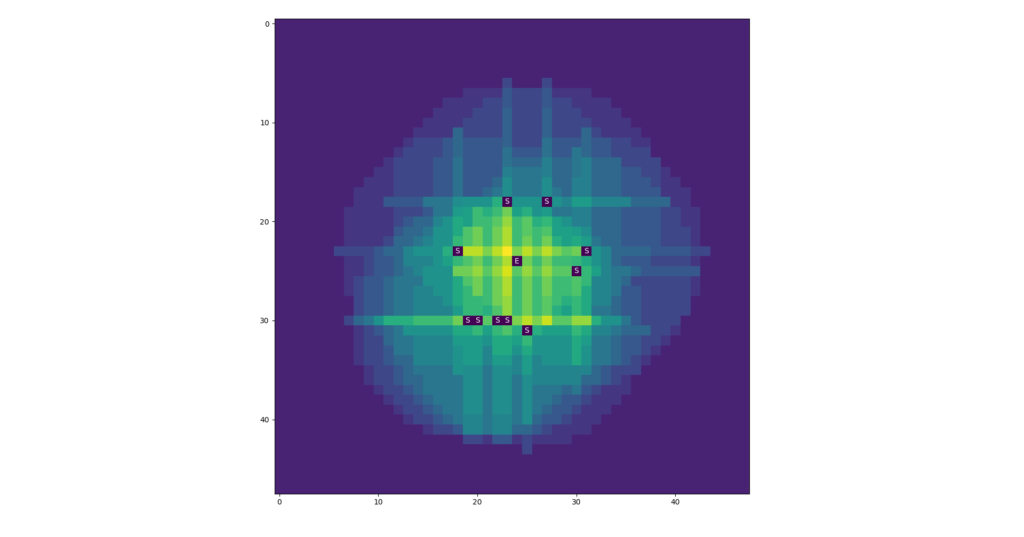
Summary
Okay, so what we want you to be able to take away from this post:
- When you’re processing data for something pointless, don’t bother being clean if doing it in a dirty way lets you figure out what matters faster
- Separate it into concerns that model, however roughly, the components that matter
- Build a metric for evaluating how good a result is
- Descend along randomly chosen positions based on how optimal they are
Feel free to ask questions or comment. The full, considerably messier code can be found here.
Leave a Reply
Only people in my network can comment.